绘制分形

分形是美丽的、引人注目的数学形式，通常可以通过一组相对简单的指令创建。在自然界中，它们可以在许多地方找到，例如海岸线、贝壳和蕨类植物，甚至被用来制造某些类型的天线。分形的数学概念为人所知已有相当长一段时间，但直到 20 世纪 70 年代，随着计算机图形学的进步和一些偶然的发现，使得伯努瓦·曼德尔布罗 (Benoît Mandelbrot)等研究人员偶然发现了分形所具有的真正神秘的可视化效果，分形才真正开始受到重视。

今天，我们将学习如何绘制这些美丽的可视化效果，并在熟悉分形背后的数学后开始自己进行一些探索，并将使用强大的 NumPy 通用函数来有效地执行必要的计算。

你会做什么

• 编写一个函数来绘制各种 Julia 集

• 创建 Mandelbrot 集的可视化

• 编写计算牛顿分形的函数

• 试验一般分形类型的变化

你将学到什么

• 对分形如何在数学上发挥作用有更好的直觉

• 对 NumPy 通用函数和布尔索引的基本了解

• 在 NumPy 中处理复数的基础知识

• 如何创建您自己独特的分形可视化

你需要什么

• Matplotlib

• make_axis_locatablempl_toolkits API 中的函数

可以按如下方式导入：

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable

• 对 Python、NumPy 和 matplotlib 有一定的了解

• 基本数学函数的概念，例如指数、sin、多项式等

• 对复数有一个非常基本的了解将会很有用

• 了解衍生品可能会有所帮助

暖身

为了对分形是什么有一些直观的了解，我们将从一个例子开始。

考虑以下等式：

\(f(z) = z^2 -1 \)

其中z是一个复数（即形式\(a + bi\)）

为了方便起见，我们将为它编写一个Python函数

def f(z):
    return np.square(z) - 1

请注意，我们使用的 square 函数是NumPy 通用函数的示例；我们很快就会回到这一决定的重要性。

为了获得对函数行为的一些直觉，我们可以尝试插入一些不同的值。

为了\(z = 0\)，我们期望得到\(-1\):

f(0)

-1

由于我们在设计中使用了通用函数，因此我们可以同时计算多个输入：

z = [4, 1-0.2j, 1.6]
f(z)

array([15.  +0.j , -0.04-0.4j,  1.56+0.j ])

有些价值会增长，有些价值会缩小，有些则不会经历太大变化。

要在更大范围内查看函数的行为，我们可以将函数应用于复平面的子集并绘制结果。为了创建我们的子集（或网格），我们可以使用meshgrid函数。

x, y = np.meshgrid(np.linspace(-10, 10, 20), np.linspace(-10, 10, 20))
mesh = x + (1j * y)  # Make mesh of complex plane

现在我们将把函数应用到网格中包含的每个值。由于我们在设计中使用了通用函数，这意味着我们可以一次性传递整个网格。这非常方便，原因有两个：它减少了需要编写的代码量并大大提高了效率（因为通用函数在计算中使用系统级 C 编程）。

在这里，我们使用3D 散点图绘制函数一次“迭代”后网格中每个元素的绝对值（或模数）：

output = np.abs(f(mesh))  # Take the absolute value of the output (for plotting)

fig = plt.figure()
ax = plt.axes(projection='3d')

ax.scatter(x, y, output, alpha=0.2)

ax.set_xlabel('Real axis')
ax.set_ylabel('Imaginary axis')
ax.set_zlabel('Absolute value')
ax.set_title('One Iteration: $ f(z) = z^2 - 1$');

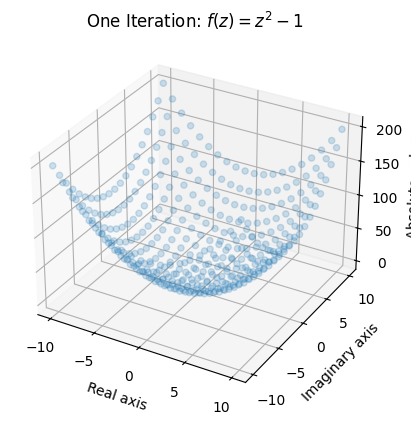
这让我们大致了解了函数的一次迭代的作用。某些区域（特别是最接近的区域）\((0,0i)\)）仍然相当小，而其他地区则增长相当大。请注意，通过取绝对值，我们会丢失有关输出的信息，但这是我们能够绘制绘图的唯一方法。

让我们看看当我们对网格应用 2 次迭代时会发生什么：

output = np.abs(f(f(mesh)))

ax = plt.axes(projection='3d')

ax.scatter(x, y, output, alpha=0.2)

ax.set_xlabel('Real axis')
ax.set_ylabel('Imaginary axis')
ax.set_zlabel('Absolute value')
ax.set_title('Two Iterations: $ f(z) = z^2 - 1$');

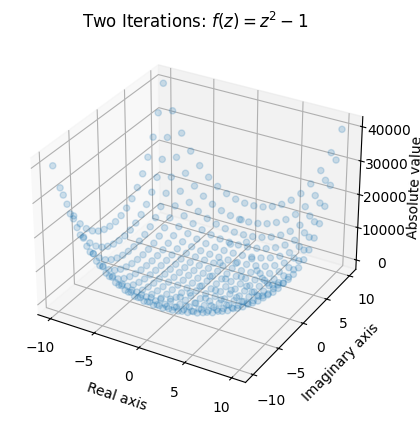
我们再次看到原点周围的值仍然很小，而具有较大绝对值（或模数）的值“爆炸”。

从第一印象来看，它的行为似乎很正常，甚至可能看起来很平常。分形往往比表面上看到的更多。当我们开始应用更多迭代时，奇异的行为就会显现出来。

考虑三个复数：

\(z_1 = 0.4 + 0.4i \),

\(z_2 = z_1 + 0.1\),

\(z_3 = z_1 + 0.1i\)

考虑到前两个图的形状，我们预计当我们对它们应用迭代时，这些值将保持在原点附近。让我们看看当我们对每个值应用 10 次迭代时会发生什么：

selected_values = np.array([0.4 + 0.4j, 0.41 + 0.4j, 0.4 + 0.41j])
num_iter = 9

outputs = np.zeros((num_iter+1, selected_values.shape[0]), dtype=complex)
outputs[0] = selected_values

for i in range(num_iter):
    outputs[i+1] = f(outputs[i])  # Apply 10 iterations, save each output

fig, axes = plt.subplots(1, selected_values.shape[0], figsize=(16, 6))
axes[1].set_xlabel('Real axis')
axes[0].set_ylabel('Imaginary axis')

for ax, data in zip(axes, outputs.T):
    cycle = ax.scatter(data.real, data.imag, c=range(data.shape[0]), alpha=0.6)
    ax.set_title(f'Mapping of iterations on {data[0]}')

fig.colorbar(cycle, ax=axes, location="bottom", label='Iteration');

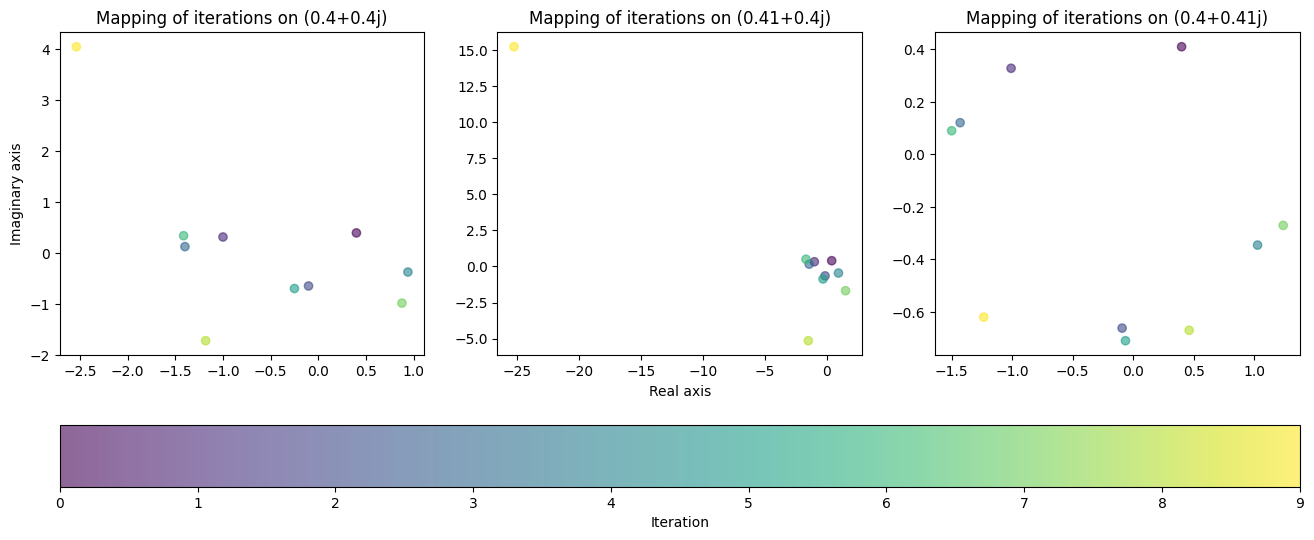
令我们惊讶的是，该函数的行为与我们的假设并不相符。这是分形所具有的混沌行为的一个典型例子。在前两张图中，值在最后一次迭代中“爆炸”，远远超出了之前包含的区域。另一方面，第三个图仍然局限于靠近原点的一个小区域，尽管值发生了微小的变化，但产生了完全不同的行为。

这给我们带来了一个极其重要的问题：在每个值发散（“爆炸”）之前可以对每个值应用多少次迭代？

正如我们从前两张图中看到的那样，值距离原点越远，它们通常爆炸得越快。尽管对于较小的值（例如\(z_1, z_2, z_3\)），我们可以假设，如果一个值与原点的距离超过一定距离（比如 2），那么它注定会发散。我们将这个阈值称为半径。

这使我们能够量化特定值的函数行为，而无需执行大量计算。一旦超过半径，我们就可以停止迭代，这为我们提供了一种回答我们提出的问题的方法。如果我们计算出发散之前应用了多少计算，我们就可以深入了解函数的行为，否则很难跟踪该行为。

当然，我们可以做得更好，设计一个在整个网格上执行该过程的函数。

def divergence_rate(mesh, num_iter=10, radius=2):

    z = mesh.copy()
    diverge_len = np.zeros(mesh.shape)  # Keep tally of the number of iterations

    # Iterate on element if and only if |element| < radius (Otherwise assume divergence)
    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        diverge_len[conv_mask] += 1
        z[conv_mask] = f(z[conv_mask])

    return diverge_len

该函数的行为乍一看可能看起来令人困惑，因此它将有助于解释一些符号。

我们的目标是迭代网格中的每个值并计算值发散之前的迭代次数。由于某些值会比其他值更快地发散，因此我们需要一个仅迭代绝对值足够小的值的过程。我们还希望一旦超过半径就停止计算值。为此，我们可以使用布尔索引，这是一种 NumPy 功能，与通用函数配合使用时是无与伦比的。布尔索引允许在 NumPy 数组上有条件地执行操作，而不必单独循环和检查每个数组值。

在我们的例子中，我们使用循环将迭代应用于我们的函数\(f(z) = z^2 -1 \)并记录。使用布尔索引，我们仅将迭代应用于绝对值小于 2 的值。

有了这些，我们就可以开始绘制我们的第一个分形了！我们将使用imshow函数创建计数的颜色编码可视化。

x, y = np.meshgrid(np.linspace(-2, 2, 400), np.linspace(-2, 2, 400))
mesh = x + (1j * y)

output = divergence_rate(mesh)

fig = plt.figure(figsize=(5, 5))
ax = plt.axes()

ax.set_title('$f(z) = z^2 -1$')
ax.set_xlabel('Real axis')
ax.set_ylabel('Imaginary axis')

im = ax.imshow(output, extent=[-2, 2, -2, 2])
divider = make_axes_locatable(ax)
cax = divider.append_axes("right", size="5%", pad=0.1)
plt.colorbar(im, cax=cax, label='Number of iterations');

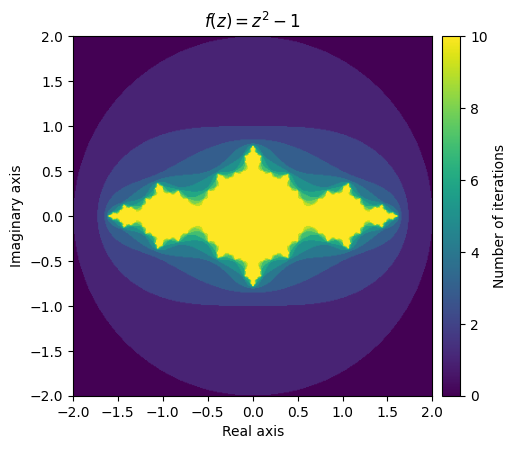
这种令人惊叹的视觉传达的是函数行为的复杂性。黄色区域代表仍然较小的值，而紫色区域代表发散的值。当您意识到它是由如此简单的函数创建的时，在趋同和发散值的边界上出现的美丽图案会更加令人着迷。

朱莉娅设定

我们刚刚探索的是特定 Julia 集的分形可视化示例。

考虑功能\(f(z) = z^2 + c\)在哪里\(c\)是一个复数。填充的 Julia集\(c\)z是函数收敛于的所有复数的集合\(f(z)\)。同样，填充的 Julia 集的边界就是我们所说的Julia 集。在上面的可视化中，我们可以看到黄色区域代表填充的 Julia 集的近似值\(c = -1\)黄绿色边框将包含 Julia 集。

为了获得更广泛的“朱莉娅分形”，我们可以编写一个函数，允许不同的值\(c\)传入：

def julia(mesh, c=-1, num_iter=10, radius=2):

    z = mesh.copy()
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        z[conv_mask] = np.square(z[conv_mask]) + c
        diverge_len[conv_mask] += 1

    return diverge_len

为了让我们的生活更轻松，我们将创建几个网格，我们将在其余示例中重复使用它们：

x, y = np.meshgrid(np.linspace(-1, 1, 400), np.linspace(-1, 1, 400))
small_mesh = x + (1j * y)

x, y = np.meshgrid(np.linspace(-2, 2, 400), np.linspace(-2, 2, 400))
mesh = x + (1j * y)

我们还将编写一个用于创建分形图的函数：

def plot_fractal(fractal, title='Fractal', figsize=(6, 6), cmap='rainbow', extent=[-2, 2, -2, 2]):

    plt.figure(figsize=figsize)
    ax = plt.axes()

    ax.set_title(f'${title}$')
    ax.set_xlabel('Real axis')
    ax.set_ylabel('Imaginary axis')

    im = ax.imshow(fractal, extent=extent, cmap=cmap)
    divider = make_axes_locatable(ax)
    cax = divider.append_axes("right", size="5%", pad=0.1)
    plt.colorbar(im, cax=cax, label='Number of iterations')

使用我们新定义的函数，我们可以再次快速绘制第一个分形：

output = julia(mesh, num_iter=15)
kwargs = {'title': 'f(z) = z^2 -1'}

plot_fractal(output, **kwargs);

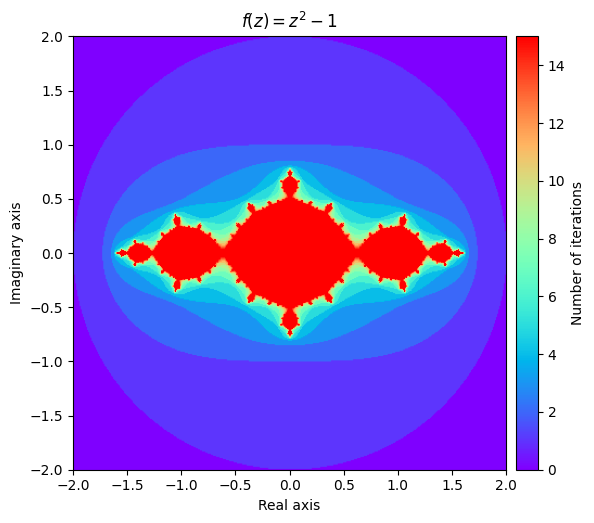
我们还可以通过尝试不同的值来探索一些不同的 Julia 集\(c\)。它对分形形状的影响之大令人惊讶。

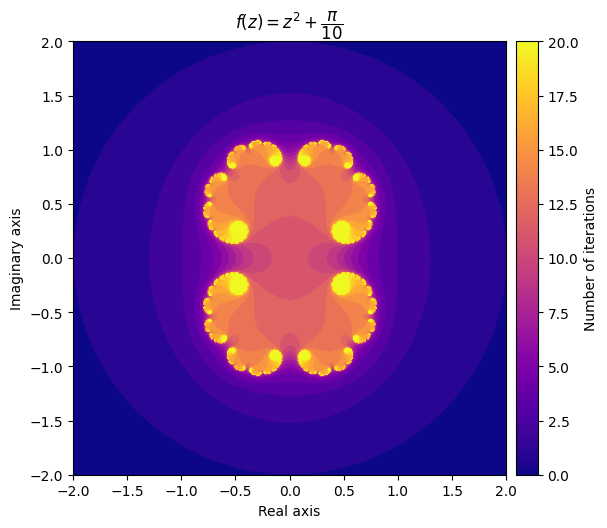
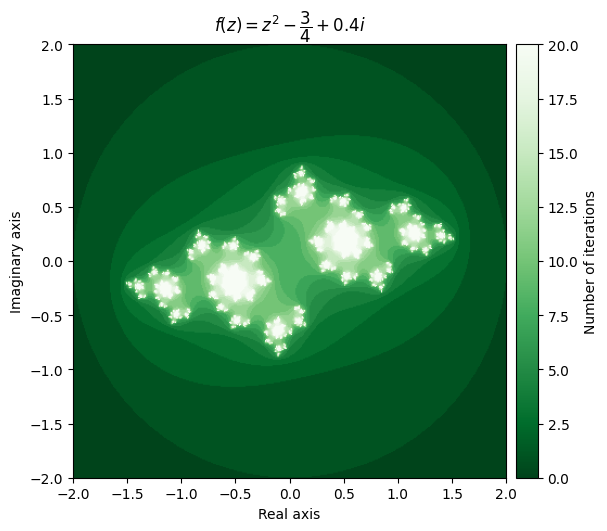
例如，设置\(c = \frac{\pi}{10}\)给我们一个非常优雅的云形状，同时设置 c =\(-\frac{3}{4} + 0.4i\)产生完全不同的模式。

output = julia(mesh, c=np.pi/10, num_iter=20)
kwargs = {'title': r'f(z) = z^2 + \dfrac{\pi}{10}', 'cmap': 'plasma'}

plot_fractal(output, **kwargs);

output = julia(mesh, c=-0.75 + 0.4j, num_iter=20)
kwargs = {'title': r'f(z) = z^2 - \dfrac{3}{4} + 0.4i', 'cmap': 'Greens_r'}

plot_fractal(output, **kwargs);

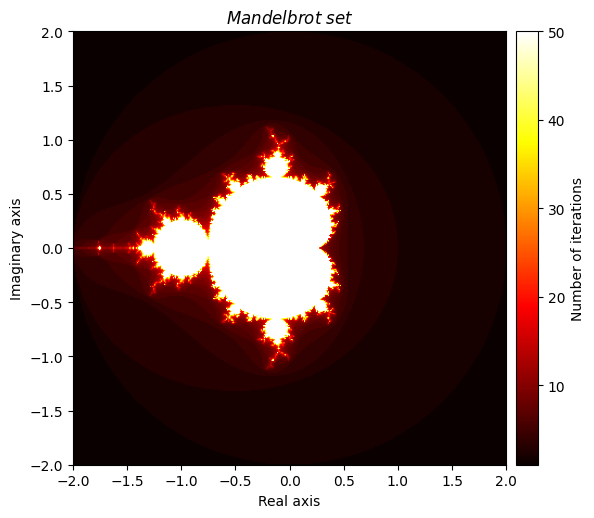
曼德尔布罗特集

与 Julia 集密切相关的是著名的Mandelbrot 集，它的定义略有不同。我们再次定义\(f(z) = z^2 + c\)在哪里\(c\)是一个复数，但这次我们的重点是我们的选择\(c\)。我们这么说\(c\)是 Mandelbrot 集的一个元素，如果 f 收敛于\(z = 0\)。一个等价的定义是说\(c\)是 Mandelbrot 集合的一个元素，如果\(f(c)\)可以无限迭代而不是“爆炸”。我们将稍微调整我们的 Julia 函数（并适当地重命名它），以便我们可以绘制 Mandelbrot 集的可视化，它拥有优雅的分形图案。

def mandelbrot(mesh, num_iter=10, radius=2):

    c = mesh.copy()
    z = np.zeros(mesh.shape, dtype=np.complex128)
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        z[conv_mask] = np.square(z[conv_mask]) + c[conv_mask]
        diverge_len[conv_mask] += 1

    return diverge_len

output = mandelbrot(mesh, num_iter=50)
kwargs = {'title': 'Mandelbrot \\ set', 'cmap': 'hot'}

plot_fractal(output, **kwargs);

推广 Julia 集

我们可以通过给它一个我们想要传入的通用函数的参数来进一步概括我们的 Julia 函数。这将允许我们绘制形式的分形\(f(z) = g(z) + c\)其中g是我们选择的通用函数。

def general_julia(mesh, c=-1, f=np.square, num_iter=100, radius=2):

    z = mesh.copy()
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < radius
        z[conv_mask] = f(z[conv_mask]) + c
        diverge_len[conv_mask] += 1

    return diverge_len

可以使用我们的通用 Julia 函数绘制的一组很酷的分形是以下形式\(f(z) = z^n + c\)对于某个正整数\(n\)。出现的一个非常酷的模式是，“突出”的区域数量与我们在迭代函数时将函数提升到的程度相匹配。

fig, axes = plt.subplots(2, 3, figsize=(8, 8))
base_degree = 2

for deg, ax in enumerate(axes.ravel()):
    degree = base_degree + deg
    power = lambda z: np.power(z, degree)  # Create power function for current degree

    diverge_len = general_julia(mesh, f=power, num_iter=15)
    ax.imshow(diverge_len, extent=[-2, 2, -2, 2], cmap='binary')
    ax.set_title(f'$f(z) = z^{degree} -1$')

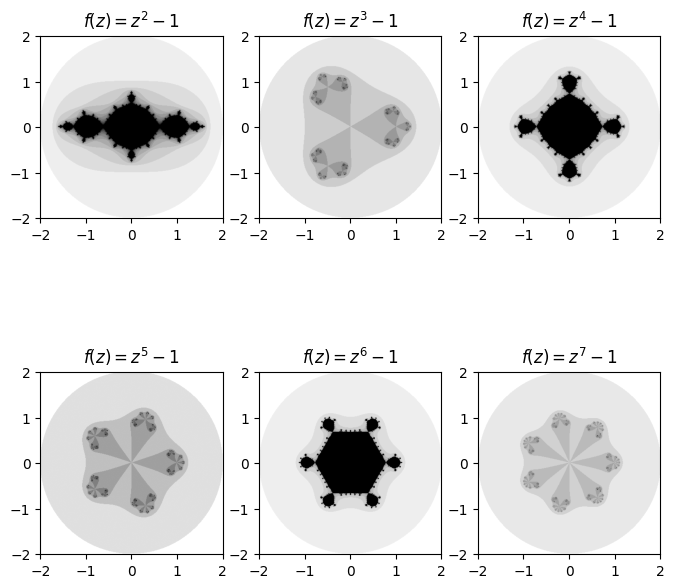
不用说，通过摆弄输入的函数、值可以完成大量的探索\(c\)、迭代次数、半径甚至网格的密度和颜色的选择。

牛顿分形

牛顿分形是一类特定的分形，其中迭代涉及添加或减go函数（通常是多项式）及其导数与输入值的比率。在数学上，它可以表示为：

\(z := z - \frac{f(z)}{f'(z)}\)

我们将定义分形的通用版本，它将允许通过传入我们选择的函数来绘制不同的变化。

def newton_fractal(mesh, f, df, num_iter=10, r=2):

    z = mesh.copy()
    diverge_len = np.zeros(z.shape)

    for i in range(num_iter):
        conv_mask = np.abs(z) < r
        pz = f(z[conv_mask])
        dp = df(z[conv_mask])
        z[conv_mask] = z[conv_mask] - pz/dp
        diverge_len[conv_mask] += 1

    return diverge_len

现在我们可以尝试一些不同的功能。对于多项式，我们可以使用NumPy Polynomial 类轻松创建绘图，该类内置了计算导数的功能。

例如，让我们尝试一个更高次的多项式：

p = np.polynomial.Polynomial([-16, 0, 0, 0, 15, 0, 0, 0, 1])
p

\[x \mapsto \text{-16.0}\color{LightGray}{ + \text{0.0}\,x}\color{LightGray}{ + \text{0.0}\,x^{2}}\color{LightGray}{ + \text{0.0}\,x^{3}} + \text{15.0}\,x^{4}\color{LightGray}{ + \text{0.0}\,x^{5}}\color{LightGray}{ + \text{0.0}\,x^{6}}\color{LightGray}{ + \text{0.0}\,x^{7}} + \text{1.0}\,x^{8}\]

其中有导数：

p.deriv()

\[x \mapsto \color{LightGray}{\text{0.0}}\color{LightGray}{ + \text{0.0}\,x}\color{LightGray}{ + \text{0.0}\,x^{2}} + \text{60.0}\,x^{3}\color{LightGray}{ + \text{0.0}\,x^{4}}\color{LightGray}{ + \text{0.0}\,x^{5}}\color{LightGray}{ + \text{0.0}\,x^{6}} + \text{8.0}\,x^{7}\]

output = newton_fractal(mesh, p, p.deriv(), num_iter=15, r=2)
kwargs = {'title': r'f(z) = z - \dfrac{(z^8 + 15z^4 - 16)}{(8z^7 + 60z^3)}', 'cmap': 'copper'}

plot_fractal(output, **kwargs)

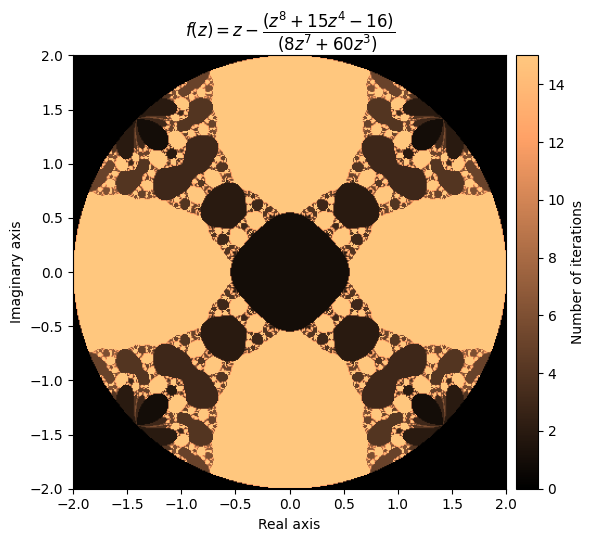
美丽的！让我们尝试另一个：

f(z) =\(tan^2(z)\)

\(\frac{df}{dz} = 2 \cdot tan(z) sec^2(z) =\frac{2 \cdot tan(z)}{cos^2(z)}\)

这使得\(\frac{f(z)}{f'(z)} = tan^2(z) \cdot \frac{cos^2(z)}{2 \cdot tan(z)} = \frac{tan(z)\cdot cos^2(z)}{2} = \frac{sin(z)\cdot cos(z)}{2}\)

def f_tan(z):
    return np.square(np.tan(z))


def d_tan(z):
    return 2*np.tan(z) / np.square(np.cos(z))

output = newton_fractal(mesh, f_tan, d_tan, num_iter=15, r=50)
kwargs = {'title': r'f(z) = z - \dfrac{sin(z)cos(z)}{2}', 'cmap': 'binary'}

plot_fractal(output, **kwargs);

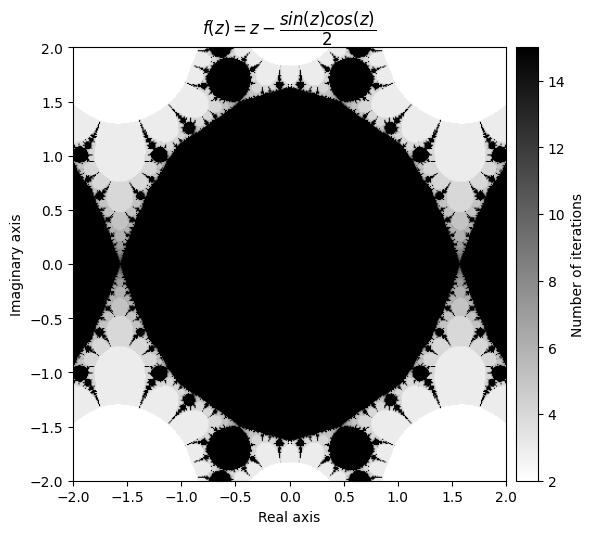
请注意，有时您必须使用半径才能获得看起来整洁的分形。

最后，我们可以对函数选择进行一些疯狂的尝试

\(f(z) = \sum_{i=1}^{10} sin^i(z)\)

\(\frac{df}{dz} = \sum_{i=1}^{10} i \cdot sin^{i-1}(z) \cdot cos(z)\)

def sin_sum(z, n=10):
    total = np.zeros(z.size, dtype=z.dtype)
    for i in range(1, n+1):
        total += np.power(np.sin(z), i)
    return total


def d_sin_sum(z, n=10):
    total = np.zeros(z.size, dtype=z.dtype)
    for i in range(1, n+1):
        total += i * np.power(np.sin(z), i-1) * np.cos(z)
    return total

我们将把这个称为“古怪的分形”，因为尝试将其方程放入标题中并不有趣。

output = newton_fractal(small_mesh, sin_sum, d_sin_sum, num_iter=10, r=1)
kwargs = {'title': 'Wacky \\ fractal', 'figsize': (6, 6), 'extent': [-1, 1, -1, 1], 'cmap': 'terrain'}

plot_fractal(output, **kwargs)

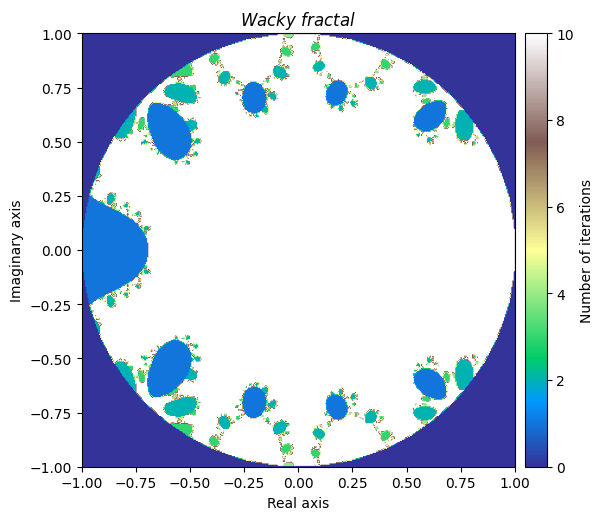
这些分形彼此之间如此独特而又相似，确实令人着迷。这将我们引向最后一部分。

创建你自己的分形

分形更令人兴奋的是，一旦您熟悉了基础知识，就有多少东西可以探索。现在，我们将通过探索一些可以尝试创建独特分形的不同方法来结束我们的教程。我鼓励您自己尝试一些事情（如果您还没有这样做）。

第一个进行实验的地方是广义 Julia 集的函数，我们可以尝试将不同的函数作为参数传递。

我们先从选择开始

\(f(z) = tan(z^2)\)

def f(z):
    return np.tan(np.square(z))

output = general_julia(mesh, f=f, num_iter=15, radius=2.1)
kwargs = {'title': 'f(z) = tan(z^2)', 'cmap': 'gist_stern'}

plot_fractal(output, **kwargs);

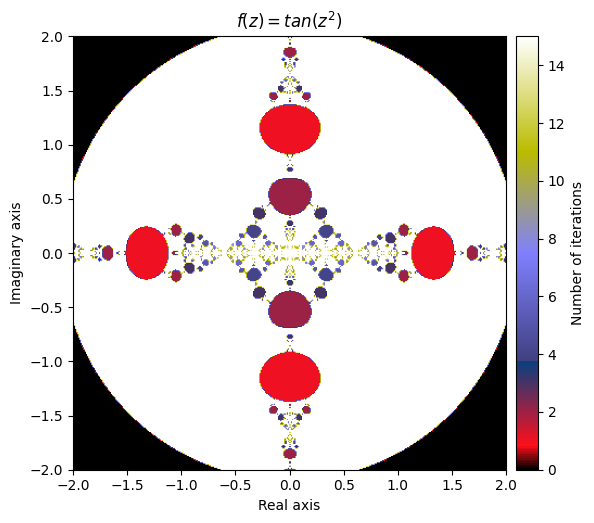
如果我们将定义的函数组合在正弦函数内会发生什么？

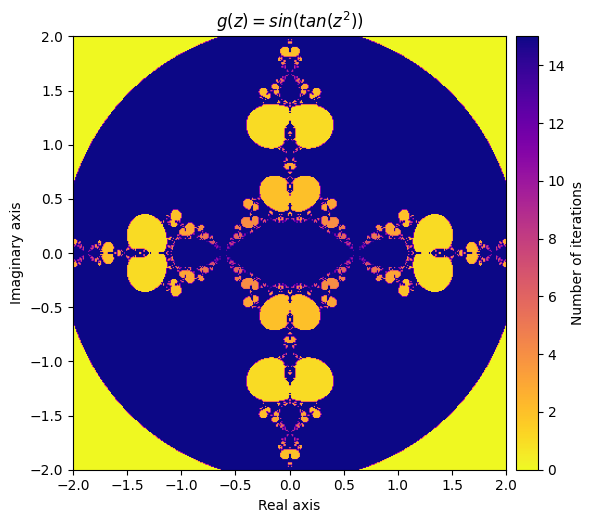
让我们尝试定义

\(g(z) = sin(f(z)) = sin(tan(z^2))\)

def g(z):
    return np.sin(f(z))

output = general_julia(mesh, f=g, num_iter=15, radius=2.1)
kwargs = {'title': 'g(z) = sin(tan(z^2))', 'cmap': 'plasma_r'}

plot_fractal(output, **kwargs);

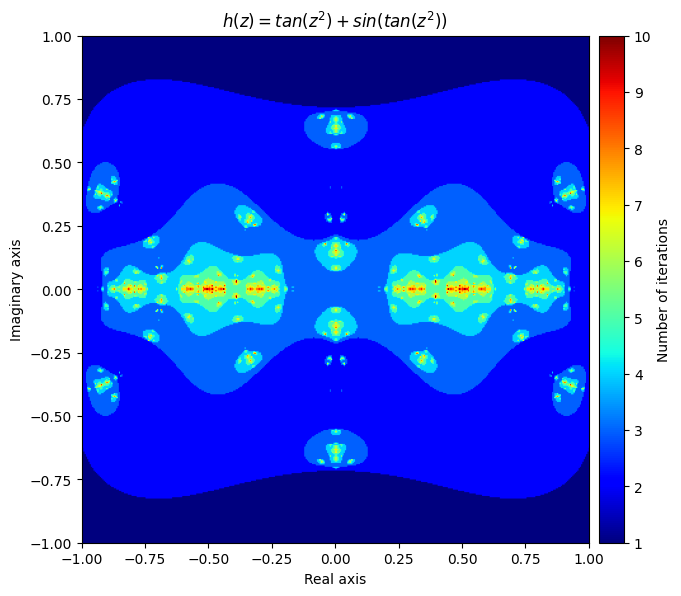
接下来，我们创建一个函数，将 f 和 g 应用于每次迭代的输入，并将结果相加：

\(h(z) = f(z) + g(z) = tan(z^2) + sin(tan(z^2))\)

def h(z):
    return f(z) + g(z)

output = general_julia(small_mesh, f=h, num_iter=10, radius=2.1)
kwargs = {'title': 'h(z) = tan(z^2) + sin(tan(z^2))', 'figsize': (7, 7), 'extent': [-1, 1, -1, 1], 'cmap': 'jet'}

plot_fractal(output, **kwargs);

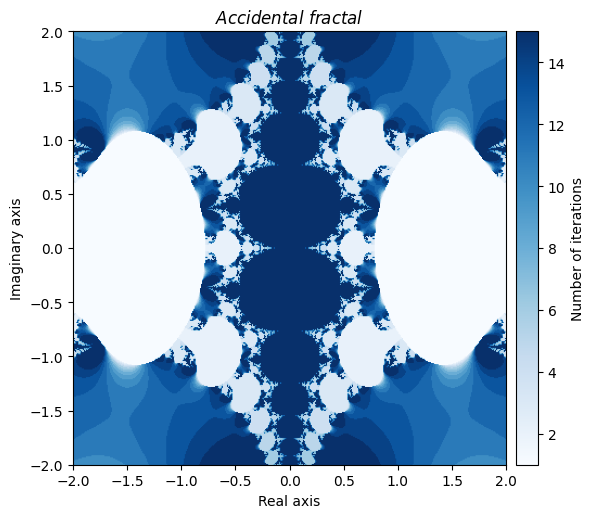
您甚至可以通过自己的错误创建美丽的分形。这是由于在计算牛顿分形的导数时犯了错误而意外创建的一个：

def accident(z):
    return z - (2 * np.power(np.tan(z), 2) / (np.sin(z) * np.cos(z)))

output = general_julia(mesh, f=accident, num_iter=15, c=0, radius=np.pi)
kwargs = {'title': 'Accidental \\ fractal', 'cmap': 'Blues'}

plot_fractal(output, **kwargs);

不用说，只需使用 NumPy 通用函数的各种组合并修改参数，就可以制作出几乎无穷无尽的有趣的分形创作。

综上所述

今天我们学到了很多关于生成分形的知识。我们看到了如何使用通用函数有效地计算需要多次迭代的复杂分形。我们还利用了布尔索引，它可以减少计算量，而无需单独验证每个值。最后，我们了解了很多关于分形本身的知识。回顾一下：

• 分形图像是通过在一组值上迭代函数并记录每个值通过特定阈值所需的时间来创建的

• 图像中的颜色对应于值的计数计数

• 填充后的朱莉娅设置为\(c\)由所有复数组成，z其中\(f(z) = z^2 + c\)收敛

• 朱莉娅设定为\(c\)是构成填充 Julia 集边界的复数集

• Mandelbrot 集是所有值\(c\)其中\(f(z) = z^2 + c\)收敛于 0

• 牛顿分形使用以下形式的函数\(f(z) = z - \frac{p(z)}{p'(z)}\)

• 当您调整迭代次数、收敛半径、网格大小、颜色、函数选择和参数选择时，分形图像可能会发生变化

靠你自己

• 尝试使用广义 Julia 集合函数的参数，尝试使用常数值、迭代次数、函数选择、半径和颜色选择。

• 访问“豪斯多夫维数分形列表”维基百科页面（在进一步阅读部分中链接）并尝试为本教程中未提及的分形编写一个函数。

进一步阅读

• 有关分形背后理论的更多信息

• 关于 Julia 集的进一步阅读

• 有关 Mandelbrot 集的更多详细信息

• 牛顿分形的更完整处理

• 不同分形的列表