numpy.geomspace #
- 麻木的。geomspace (开始,停止, num = 50 ,端点= True , dtype = None , axis = 0 ) [来源] #
返回在对数刻度上均匀分布的数字(几何级数)。
这与 类似
logspace,但直接指定端点。每个输出样本都是前一个样本的常数倍。版本 1.16.0 中进行了更改:现在支持非标量启动和停止。
- 参数:
- 开始类似数组
序列的起始值。
- 停止类似数组
序列的最终值,除非端点为 False。在这种情况下,值在日志空间的间隔内间隔开,其中除了最后一个(长度为num的序列)之外的所有值都会被返回。
num + 1- num整数,可选
要生成的样本数。默认值为 50。
- 端点布尔值,可选
如果为 true,则 stop是最后一个样本。否则,不包括在内。默认为 True。
- 数据类型数据类型
输出数组的类型。如果未给出,则从start和stop
dtype推断数据类型。推断的 dtype 永远不会是整数;即使参数会生成整数数组,也会选择float 。- 轴int,可选
结果中用于存储样本的轴。仅当开始或停止类似于数组时才相关。默认情况下 (0),样本将沿着在开头插入的新轴。使用 -1 在末端获取轴。
1.16.0 版本中的新增内容。
- 返回:
- 样本ndarray
num个样本,在对数刻度上等距分布。
也可以看看
logspace与 geomspace 类似,但使用 log 和 base 指定端点。
linspace与 geomspace 类似,但使用算术而不是几何级数。
arange与 linspace 类似,指定步长而不是样本数。
- 如何创建具有规则间隔值的数组
笔记
如果输入或数据类型为复数,则输出将遵循复平面中的对数螺线。 (有无数条螺旋线穿过两个点;输出将遵循最短的此类路径。)
例子
>>> np.geomspace(1, 1000, num=4) array([ 1., 10., 100., 1000.]) >>> np.geomspace(1, 1000, num=3, endpoint=False) array([ 1., 10., 100.]) >>> np.geomspace(1, 1000, num=4, endpoint=False) array([ 1. , 5.62341325, 31.6227766 , 177.827941 ]) >>> np.geomspace(1, 256, num=9) array([ 1., 2., 4., 8., 16., 32., 64., 128., 256.])
请注意,上述可能不会产生精确的整数:
>>> np.geomspace(1, 256, num=9, dtype=int) array([ 1, 2, 4, 7, 16, 32, 63, 127, 256]) >>> np.around(np.geomspace(1, 256, num=9)).astype(int) array([ 1, 2, 4, 8, 16, 32, 64, 128, 256])
允许负数、递减和复数输入:
>>> np.geomspace(1000, 1, num=4) array([1000., 100., 10., 1.]) >>> np.geomspace(-1000, -1, num=4) array([-1000., -100., -10., -1.]) >>> np.geomspace(1j, 1000j, num=4) # Straight line array([0. +1.j, 0. +10.j, 0. +100.j, 0.+1000.j]) >>> np.geomspace(-1+0j, 1+0j, num=5) # Circle array([-1.00000000e+00+1.22464680e-16j, -7.07106781e-01+7.07106781e-01j, 6.12323400e-17+1.00000000e+00j, 7.07106781e-01+7.07106781e-01j, 1.00000000e+00+0.00000000e+00j])
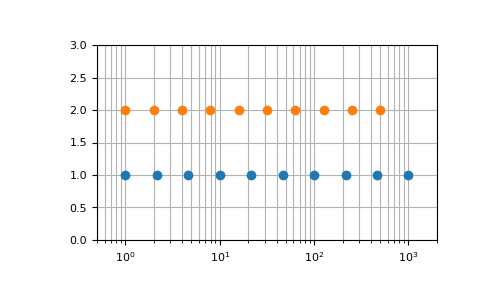
端点参数图解:
>>> import matplotlib.pyplot as plt >>> N = 10 >>> y = np.zeros(N) >>> plt.semilogx(np.geomspace(1, 1000, N, endpoint=True), y + 1, 'o') [<matplotlib.lines.Line2D object at 0x...>] >>> plt.semilogx(np.geomspace(1, 1000, N, endpoint=False), y + 2, 'o') [<matplotlib.lines.Line2D object at 0x...>] >>> plt.axis([0.5, 2000, 0, 3]) [0.5, 2000, 0, 3] >>> plt.grid(True, color='0.7', linestyle='-', which='both', axis='both') >>> plt.show()